02. 微分概要

微分概要

在上一课，你学习了 导数 。本节课只是复习过去学到的知识。

理解导数

你了解到了一些理解导数的方法。

1. 对"变化率"的解释

如果 f(t) 给出了在 任何 t 的值，那么 \dot{f}(t_0) 会给出 f(t) 在数值 t=t_0 的变化率。


2. 图形解释

与 f(t) 在 t=t_0 相切的直线的斜率是 \dot{f}(t_0) 。


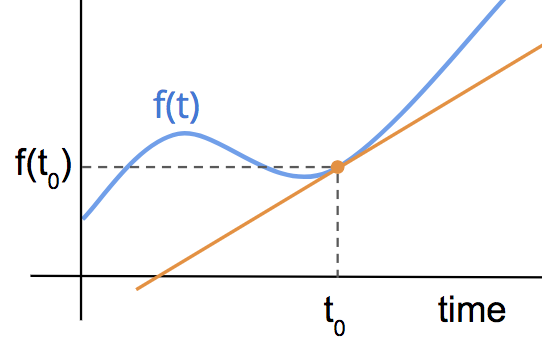
橙色线的斜率等于*f*在 t = t_0 处的**导数**。

橙色线的斜率等于 f 在 t = t_0 处的 导数 。

3. 正式定义

正式的 数学定义如下：

函数 f(t) 的 导数 是函数 \dot{f}(t) (or \frac{df}{dt} )，定义为：

\dot{f}(t) = \lim_{\Delta t \to 0}\frac{ f(t + \Delta t) - f(t)}{\Delta t}


导数和运动

位置 、 速度 和 加速度 在描述车辆的运动时都是有用的量，这些量通过导数相互关联。

  • 速度是位置的导数

  • v(t)=\dot{x}(t)

  • 加速度是速度的导数和位置的二阶导数。

  • a(t) = \dot{v}(t) = \ddot{x}(t)

编码导数 

def get_derivative_from_data(position_data, time_data):
    """
    Calculates a list of speeds from position_data and
    time_data.

    Arguments:
      position_data - a list of values corresponding to
        vehicle position

      time_data     - a list of values (equal in length to
        position_data) which give timestamps for each
        position measurement

    Returns:
      speeds        - a list of values (which is shorter
        by ONE than the input lists) of speeds.
    """
    # 1. Check to make sure the input lists have same length
    if len(position_data) != len(time_data):
        raise(ValueError, "Data sets must have same length")

    # 2. Prepare empty list of speeds
    speeds = []

    # 3. Get first values for position and time
    previous_position = position_data[0]
    previous_time     = time_data[0]

    # 4. Begin loop through all data EXCEPT first entry
    for i in range(1, len(position_data)):

        # 5. get position and time data for this timestamp
        position = position_data[i]
        time     = time_data[i]

        # 6. Calculate delta_x and delta_t
        delta_x = position - previous_position
        delta_t = time - previous_time

        # 7. Speed is slope. Calculate it and append to list
        speed = delta_x / delta_t
        speeds.append(speed)

        # 8. Update values for next iteration of the loop.
        previous_position = position
        previous_time     = time

    return speeds

Next Concept